Tales de Mileto genio, matemático y astrónomo. Es considerado el primer filósofo de la historia por indagar racionalmente sobre el origen del Universo, que para él, era un espacio racional pese a su aparente desorden
[flagallery gid=25 name=Gallery]
Sin embargo, no buscó un Creador en dicha racionalidad, pues para él todo nacía del agua, la cual era el elemento básico del que estaban hechas todas las cosas, pues se constituye en vapor, que es aire, nubes y éter; del agua se forman los cuerpos sólidos al condensarse, y la Tierra flota en ella. La Tierra, para él, era un disco plano cubierto por la semiesfera celeste flotando en un Océano infinito.
La explicación simplista basada más en la reflexión que en la contrastación que deja en el aire interrogantes relativas al sol, los planetas o las estrellas; pero que sin embargo supone un gran avance con respecto al Universo homérico en donde los dioses en las alturas del Olimpo o los infiernos bajo la tierra marcaban la vida de los mortales.
Es considerado uno de los siete sabios de Grecia, (junto a Bias, Solón, Quilón, Pítaco, Cleóbulo y Periandro).
Fue hijo de Euxamias y de Cleobulina. Se cree que nación en Mileto (colonia griega del Asia Menor) en el año 624 a.C, y falleció en el 546 a.C, pero los historiadores no se ponen de acuerdo. Fue legislador de esa ciudad.
Tales buscaba el Primer Principio de Todas las Cosas, el principio del que todo proviene y al que todo regresa y del que cada cosa particular no es sino una variación.
El principal mérito de Tales fue haber buscado, basándose sólo en la razón y la experiencia, el principio originario de todo ser. De este modo transformó en tema de reflexión crítica la visión que todo hombre tiene del mundo y de la vida.
Tales afirmo que «todo está lleno de dioses». Esta frase ha sido interpretada de múltiples formas. Unos historiadores la comentan como que el mundo está lleno de energía, de fuerzas; como cuando afirmaba que el imán tiene alma porque atrae al hierro. Otros que el agua daba cuenta del mundo de las cosas pero nada decía de la condición personal del hombre que, no queriendo quedarse solo en un mundo de meros objetos, no estaba dispuesto a renunciar a sus dioses. Creía que la caída de un rayo no tenía por qué ser adjudicada a la cólera del dios griego Zeus.
Ninguno de sus escritos ha llegado hasta nuestros días; a pesar de ello, son muy numerosas las aportaciones que a lo largo de la historia, desde Heródoto, Jenófanes o Aristóteles, se le han atribuido. En la Biblioteca de Alejandría no se encontró ninguna obra suya si se exceptúa una de muy dudosa procedencia: Astrología Náutica, la cual, según Laercio, pertenecía a Foco el Samio.
Según los testimonios que se conservan de Aristóteles, éste le adjudica la creación de la escuela jonia de filosofía y entre sus discípulos podemos citar a Pitágoras, Anaxímedes o Anaximandro.
Tales de Mileto se vinculo profundamente con el estudio de la Geometría, Dinámica, Óptica, Estática, Álgebra lineal y Geometría espacial. Llegó a afirmar que el primer principio es el agua y dijo que “el Océano es Osiris y Tetis es Isis”, y que de ella proviene todo por condensación y dilatación.
Diógenes Laercio afirma que Tales llego a Mileto luego de haber sido expulsado de Fenicia. Lo cierto es que el filósofo sí vivió en Fenicia.
Se cree que el joven Tales visitaba asiduamente Egipto y recibió educación por parte de los sacerdotes, Menfis y Dióspolis. Por otro lado se estima que el origen de sus conocimientos astronómicos se debe a la influencia de los babilonios.
Según los testimonios de Diógenes Laercio se le considera como el primer filósofo en aseverar la existencia de un alma inmortal, pensamientos que luego tomaría Aristóteles para la creación de su teoría. Heródoto por su parte afirmaba que Tales fue capaz de desviar el curso del río Halys para que el ejército de Creso pudiera llegar a la otra orilla.
Aristóteles documentó en (Política) que Tales era además muy hábil para los negocios. Destaca que cierta vez compró prensas de aceite de oliva de Mileto y Quíos y, llegado el momento de la abundante cosecha, alquiló dichas maquinarias a los recolectores haciéndose así con una buena fortuna. Aunque la riqueza no era su principal meta en la vida.
Otros pensadores de la época cuentan que Tales fue capaz de predecir a los jónicos la llegada de un eclipse de sol, que oscureció una parte de Oriente Próximo y Egipto; que fue el responsable de descubrir la altura exacta de las pirámides egipcias usando como guías las sombras proyectadas en comparación con las del cuerpo humano y se le adjudica, además, la división del año en 365 días con sus correspondientes estacionesy la división de un círculo por su diámetro en dos mitades iguales, la predicción de un eclipse.
Por su parte Heródoto considera a Tales práctico, capaz de realizar las más audaces creaciones de ingeniería y de un hombre hábil para la política, pero ante todo Tales de Mileto es un científico con profundos conocimientos de astronomía y matemáticas. Fue el primero que intentó dejar de lado las explicaciones sobrenaturales para dar cuenta de los fenómenos cotidianos visibles en la naturaleza.
No contento con medir las cosas que circunscriben a la tierra, Tales estaba también intrigado con el cielo, y se dio cuenta de que el sol, la luna y las estrellas, se movían con una notable regularidad.
Se le atribuye haber sido la primera persona en ubicar el grupo de estrellas conocido como Osa Mayor, o El Carro, y de usarlo en navegación.
Cuando en geometría hablemos del Teorema de Thales, debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto.
Teorema de Thales
El primero de ellos se refiere a la construcción de un triángulo que sea semejante a otro existente (triángulos semejantes son los que tienen iguales ángulos).
Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (los circuncentros se encuentran en el punto medio de su hipotenusa).
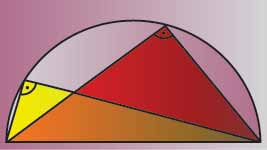Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos.
